How To Decide If Zero Inflated Model Fits The Data

Proportion and pct information are catchy to clarify.

Much like count data, they look like they should work in a linear model.

They're numerical. They're oft continuous.

And sometimes they do work. Some proportion data do expect commonly distributed then estimates and p-values are reasonable.

But more oft they don't. So estimates and p-values are a mess. Luckily, there are other options. One is beta regression.

Beta Regression

Like logistic and Poisson regression, beta regression is a type of generalized linear model.

It works nicely for proportion information because the values of a variable with a beta distribution must fall between 0 and ane.

It's a scrap of a funky distribution in that information technology'southward shape can modify a lot depending on the values of the mean and dispersion parameters.

Here are a few examples of the possible shapes of a beta distribution, with different means and variances:

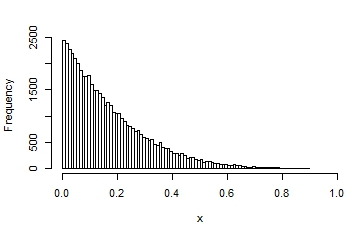
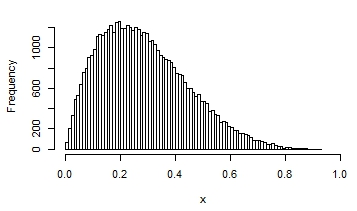
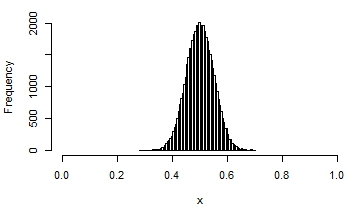
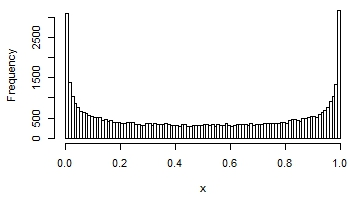
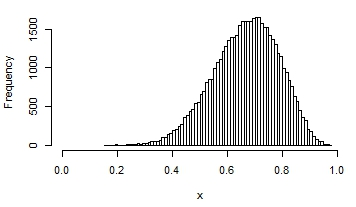
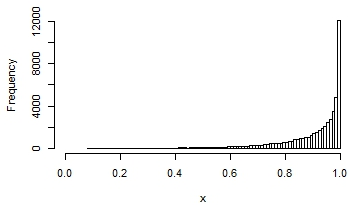
You can see that in some, the distribution looks quite normal. It that situation, you would get reasonable estimates and p-values if you assumed normality.

But here is just the kind of viscid situation yous commonly meet in real data. Let's say you desire to compare the hateful proportion of days out of 30 that people exercise some behavior–take their prescribed medication, exercise for at least 30 minutes, or act physically aggressively toward peers.

Peradventure you've got some intervention that you desire to test volition help people take their medications. Perhaps the control grouping indeed looks like the nice normal distribution in the tertiary graph in a higher place.

Just the treatment worked so well that in the intervention grouping, the distribution is highly skewed. Information technology looks like the final graph.

Assuming normality isn't going to work here. That's where a beta regression can piece of work instead.

One big problem.

0 and 1 aren't possible values in a beta distribution. Then if Y|X follows a beta distribution, Y can take values shut to 0 and one, say .001 or .998. Simply not 0 or 1 exactly.

Then if a client takes their medication 30 out of 30 days, a beta regression won't run. You can't have any 0s or 1s in the data fix.

Zero-One Inflated Beta Models

There is, however, a version of beta regression model that can work in this situation. It'southward ane of those models that has been around in theory for a while, but is only in the by few years become available in (some) mainstream statistical software.

It's chosen a Nil-1-Inflated Beta and information technology works very much like a Zero-Inflated Poisson model.

Information technology's a type of mixture model that says there are really three processes going on.

1 is a process that distinguishes between zeros and non-zeros. The idea is in that location is something qualitatively different well-nigh people who never accept their medication than those who do, at least sometimes.

Likewise, there is a procedure that distinguishes between ones and not-ones. Again, at that place is something qualitatively different nigh people who always accept their medication than those who do sometimes or never.

So at that place is a third process that determines how much someone takes their medication if they practice some of the time.

The first and second processes are run through a logistic regression and the third through a beta regression.

These three models are run simultaneously. They can each take their own prepare of predictors and their own set of coefficients. For instance, maybe memory is a big predictor of how oft someone takes their medication if they take it sometimes, merely not at all an issue for whether or not someone takes it 0 times. Perhaps those people aren't forgetting–they can't afford to purchase it.

So maybe whether someone has health insurance that pays for the medication is a predictor in the zero/non-zippo logistic regression, only not in the other two parts.

Depending on the shape of the distribution, you may not demand all iii processes. If there are no zeros in the data set, you may only need to accommodate inflation at 1.

It'due south highly flexible and adds important options to your data analysis toolbox.

Delight annotation that, due to the large number of comments submitted, any questions on issues related to a personal study/projection volition not be answered. We suggest joining Statistically Speaking, where you take access to a private forum and more resource 24/vii.